Coursera Machine Learning 정리 (한글) - Week 1
in Programming
- 이 포스트는 Coursera에서 제공하는 Andrew Ng 교수님의 Machine Learning week 1 강의 요점을 한국어로 정리한 것입니다.
- 해당 강의는 Coursera 공식 사이트에서 무료로 수강할 수 있습니다.
- 오역 및 오탈자를 제보해 주세요. 감사합니다.
1. Introduction
1.1 Welcome
데이터의 축적, 컴퓨터 성능의 발전, AI 연구의 발전 등으로 인해 머신 러닝 분야가 성장하고 있으며 현재 많은 분야의 산업에서 머신 러닝을 사용하고 있다. 대표적인 적용 분야는 다음과 같다.
- 데이터베이스 마이닝
(ex: 유저의 웹 클릭 데이터를 이용한 서버 로드 밸런싱 시스템) - 직접 코딩할 수 없는 애플리케이션
(ex: 자연어 처리, 컴퓨터 비전) - 개인 맞춤 서비스
(ex: 아마존의 상품 추천, 넷플릭스의 영화 추천 시스템) - 실제 인간 뇌 작용의 이해
1.2 What is machine learning?
머신 러닝은 크게 두 가지 방식으로 정의할 수 있다. 하나는 오래되고 비공식적인 표현으로 다음과 같다.
머신 러닝은 컴퓨터에게 배울 수 있는 능력, 즉 코드로 정의하지 않은 동작을 실행하는 능력에 대한 연구 분야이다. (Arthur Samuel, 1959)
한편, Tom Mitchell은 조금 더 현대적인 정의를 제시한다.
잘 제안된 학습 문제는 다음과 같다 : 어떤 과제 T(Task)에 대한 성능이 P(Performance)라고 측정되고 경험 E(Experience)를 통해 향상된다면, 프로그램은 과제 T에 대해 경험 E로부터 성능 기준 P에 따라 학습한다고 할 수 있다. (Tom Mitchell, 1998)
예를 들어 체커 게임을 한다고 했을 때 E는 많은 체커 게임을 했던 기록으로, T는 체커를 하는 작업으로, P는 프로그램이 다음 게임에서 이길 확률로 나타낼 수 있다.
1.3 Supervised Learning
지도 학습(supervised learning)은 학습용 데이터 샘플과 그에 해당하는 출력이 함께 제공되는 학습 방식이다.
지도 학습은 회귀(regression) 문제와 분류(classification) 문제로 나눌 수 있다. 회귀 문제에서는 연속적(continuous) 출력 값을 예측하고 분류 문제에서는 이산적(discrete) 출력 값을 예측한다는 데서 차이를 보인다.
부동산에서 집의 크기가 주어졌을 때 그 집의 가격을 예측하는 문제가 있다고 하자. 출력이 가격(ex: 2억 원, 2억 5천만 원, …), 즉 연속적인 값으로 나타나야 하므로 이 문제는 회귀 문제이다.
반면에 집의 크기가 주어졌을 때 특정 가격(ex: 2억 2천만 원)보다 높게 혹은 낮게 팔 수 있을지 여부를 예측하는 문제가 주어진다고 하자. 출력이 두 개의 카테고리(높음, 낮음)로 나타나야 하므로 이 문제는 분류 문제이다.
1.4 Unsupervised Learning
비지도 학습(unsupervised learning)은 학습용 데이터 샘플만 주어지고 출력이 주어지지 않는 학습 방식이다.
비지도 학습은 결과값이 어떻게 될지 인위적으로 예측하기 힘든 문제에 접근하게 해 준다. 비지도 학습을 통해 데이터의 각 변수들 간의 관계성을 파악하여 데이터를 클러스터링하는 등의 활동이 가능하다. 또한 비지도 학습은 결과값에 따른 피드백이 불가능하다.
1,000,000개의 서로 다른 유전자를 유사성에 따라 그룹화하는 문제가 있다. 이 문제는 클러스터링 문제로 비지도 학습으로 해결할 수 있다.
칵테일 파티 알고리즘은 시끄러운 환경 속에서 특정 사람의 목소리만 추출하는 문제에 대한 알고리즘으로, 이 문제는 비 클러스터링 문제이지만 비지도 학습으로 해결할 수 있다.
2. Model and Cost Function
2.1 Model Representation
이 강의에서는 입력 변수를 \(x^{(i)}\) 로, 출력 변수를 \(y^{(i)}\) 로 표기한다. 입력과 출력 변수의 쌍은 \((x^{(i)}, y^{(i)})\) 로 표기한다. 지수 \((i)\) 는 학습 데이터의 인덱스를 가리키는 것이다. 입력 변수 전체의 공간을 X로, 출력 변수 전체의 공간을 Y로 표기한다.
지도 학습에서 우리의 목표는 학습 데이터 세트가 주어졌을 때 함수 h : X → Y를 “잘” 학습시키는 것으로, 여기에서 함수 h는 가설(hypothesis)이라고 부른다. h를 학습시키는 프로세스를 그림으로 요약하자면 다음과 같다:
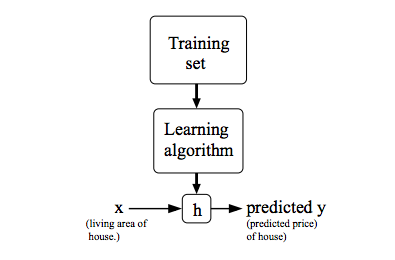
2.2 Cost Function
가설 함수의 정확성을 비용 함수(cost function)를 통해 측정할 수 있다. 비용 함수는 데이터 쌍의 예측 출력치와 실제 출력치의 차이의 제곱을 평균하고 \(\frac{1}{2}\)을 곱한 것으로 다음과 같이 나타내어진다. \[J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^{m} (\hat{y}_i - y_i)^2 = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x_i)-y_i)^2\]
이 함수는 제곱 오차 함수(squared error function)나 평균 제곱 오차(mean squared error)라고도 부른다. 비용 함수에 \(\frac{1}{2}\)을 곱한 것은 후술할 경사 감소(gradient descent)의 계산의 편의성 때문으로, 추후 오차 제곱 항을 미분하였을 때 2가 나오므로 \(\frac{1}{2}\)이 상쇄된다.
2.3 Cost Function - Intuition I
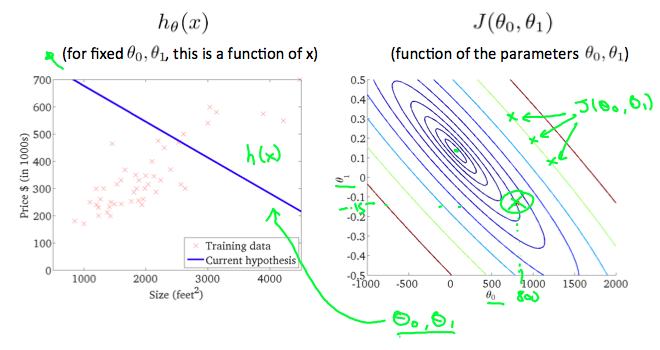
시각적으로 표현하기 위해 모든 학습 데이터 세트가 x-y 평면에 존재한다고 가정하고, 이 모든 데이터 세트를 지나가는 직선을 만든다고 생각해 보자.
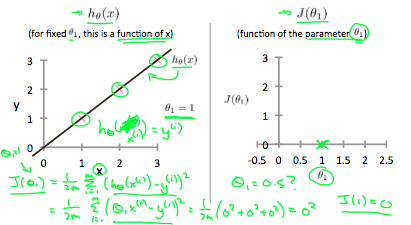
가능한 한 가장 좋은 선을 그리기 위해서는, 모든 데이터와 선 사이의 직선 거리의 제곱의 총합이 최소가 되어야 한다. 이상적인 경우 직선이 모든 데이터를 지나가게 되는데 이 경우 비용 함수, 즉 \(J(\theta_0, \theta_1)\)이 0이 된다.
반면에 왼쪽 그림에서 \(\theta_1 = 0.5\)인 경우 직선 거리가 늘어나 비용 함수도 같이 늘어나는 것을 관찰할 수 있다.
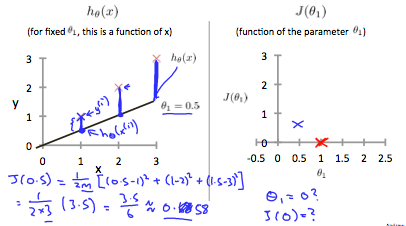
이런 식으로 \(\theta_1\)의 값을 조정하여 오차 함수의 변화를 관찰하면 다음과 같은 그래프를 그릴 수 있다.
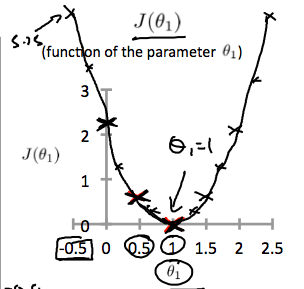
결과적으로 \(\theta_1 = 1\)일 때 비용 함수가 최소가 되어 \(\theta_1 = 1\) 이 전역 최소값이 된다.
2.4 Cost Function - Intuition II
여러 등고선으로 이루어진 그래프를 등고선 그래프(contour plot) 라고 한다. 한 등고선 안의 모든 점은 일정한 값(그림에서는 비용 함수)을 가지며, 등고선 그래프의 중점에서는 최소 비용 함수값을 가진다.
3. Parameter Learning
3.1 Gradient Descent
경사 하강법(Gradient Descent)은 비용 함수에 대하여 가설 함수의 파라미터들을 최적화하기 위해 사용되는 알고리즘이다. \(\theta_0\)를 x축에, \(\theta_1\)을 y축에, 그리고 비용 함수를 z축으로 설정한 그래프가 다음과 같이 주어진다고 가정하자.
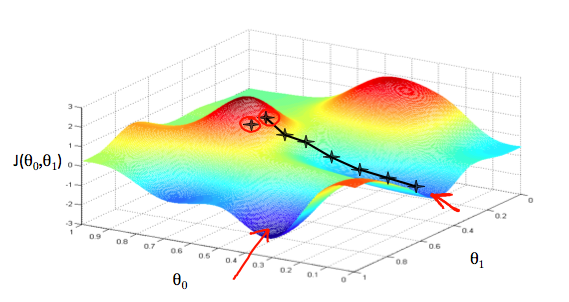
파라미터의 시작점을 빨간 동그라미라고 하자. 비용 함수를 최소화시키기 위해서는 그래프에서 z축이 최소가 되는 위치로 파라미터를 조정해야 한다. 이를 위해 우리는 비용 함수를 미분하여 문제를 해결할 수 있다. 특정 위치에서의 비용 함수의 기울기(검은 선의 방향)를 구하여 그 방향으로 조금씩 이동하면 비용 함수의 최소값에 도달하게 된다. 각 단계마다 이동하는 거리는 하이퍼파라미터 \(\alpha\) 에 의하여 결정되는데, 이를 학습률(learning rate)이라고 한다.
만약 시작점이 다른 경우(왼쪽 빨간 동그라미에서 시작할 경우) 다른 점으로 수렴하게 될 수 있다. 이 때 수렴하는 지점을 지역 최소값(local minima)이라고 한다.
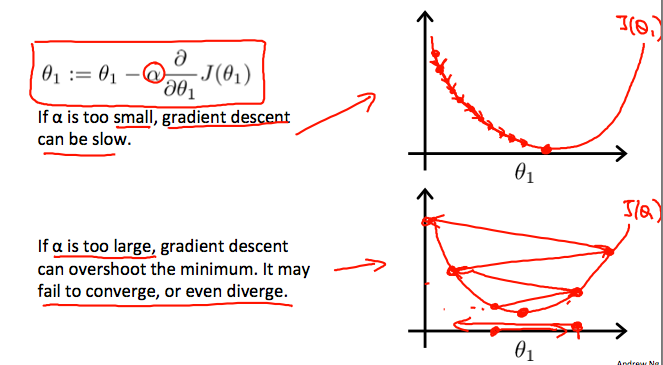
즉, 경사 하강법은 각 파라미터에 대하여 다음 알고리즘이 수렴할 때까지 수행하는 것이다: \[\theta_j := \theta_j - \alpha\frac{\partial}{\partial \theta_j}J(\theta_0, \theta_1)\]
3.2 Gradient Descent Intuition
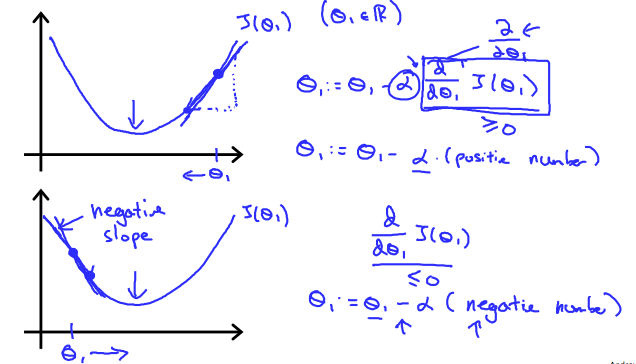
파라미터가 \(\theta_1\) 하나일 때를 가정하자. 비용 함수의 최소값으로의 방향인 \(\frac{d}{d \theta_1}J(\theta_1)\) 의 부호에 관계없이 \(\theta_1\) 은 결국 비용 함수의 최소값으로 수렴하게 된다. 미분값이 음수라면 \(\theta_1\) 은 증가하고, 반대로 미분값이 양수라면 \(\theta_1\) 은 감소한다.
경사 하강법의 수렴 과정에서 학습률이 너무 낮다면 최소값까지 수렴하는 데 필요한 반복 과정이 지나치게 많아질 수 있다. 반대로 학습률이 너무 높다면 함수는 수렴하지 못하거나 발산할 수도 있다.
3.3 Gradient Descent For Linear Regression
경사 하강법 공식을 다음과 같이 수정할 수 있다: \[\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_\theta (x_i)-y_i)\]
이 식은 비용 함수 \(J(\theta)\)의 편미분항을 전개하여 정리한 것이며, 그 과정은 다음과 같다:
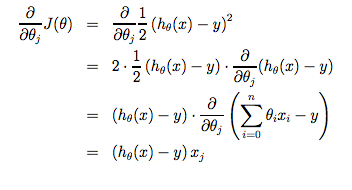
지금까지 서술한 이 방법은 한 단계마다 모든 학습 데이터 세트를 사용하는 방식으로 배치 경사 하강법(batch gradient descent)이라고 부른다. 경사 하강법이 일반적으로 지역 최소값에 민감하긴 하지만, 여기에서 제기한 문제는 하나의 전역 최소값만 가지고 있기 때문에 경사 하강법이 언제나 전역 최소값으로 수렴한다는 점에 주목하라.
